For me, this week has consisted of more noise work! With the main focus concerning the low frequency variation of intensity along a yarn. Also there are some concerns from the previous noise implementation regarding aliasing.

Aliasing and the intensityVariation (cell noise)

In the previous post about intensityVariation i did not consider aliasing and other sampling related issues. The rendering engine will sample an area a number of times. From the sampling theorom we know that in order to fully capture a signal the sampling frequency must be twice that of the maximum frequency of the signal.

Having a shader which introduces high-frequency content can be problematic since it requires many more samples in order to avoid aliasing in the result. Also the nature of the entire shader of having detailed threads in very samll scale already is of high frequency and will result in aliasing.

I think it would be good to investigate this and decide what is acceptable and what should be avoided. Since some alliasing effects might be desirable since they also occur in photography.

The noise touched upon in the remaining text of this post is low frequency and can be controlled to be bandlimited.

Variation along yarns.

Some fabrics have characteristic streaks when viewed from far.

A good example of this can be seen in the following picture (taken from here):

These streaks arise because of variations in color along the lengths of the individual yarns.

To simulate this we can use noise to vary the intensity along the length of the strands of yarn. But just using random numbers will be much to erratic to give the desired result. Instead much smoother noise is required to give the variation a natural behaviour.

A common tool in the field of computer graphics to introduce some variation is Perlin noise. This gives smooth noise which can be controlled using parameters to give random behaviour and variation that looks natural.

First the algorithm for producing these random values had to be implemented.

Perlin noise

I found a number of sources for information this post, Ken Perlins own implementation as well as the chapter on it in pbrt.

The algorithm devides scaled input \(x, y, z\) coordiantes into unit cubes and relative coordinates of the current point in the current unit cube are calculated.

    static double noise(double x, double y, double z) {
        // index of unit cube
        int X = (int)floor(x) & 255;
        int Y = (int)floor(y) & 255;
        int Z = (int)floor(z) & 255;

        // relative coords in unit cube
        x -= floor(x);
        y -= floor(y);
        z -= floor(z);
    
        ...

    }

These relative coordinates are then transformed/distored using the function \( y(x) = 6 t^6 - 15 t^4 + 10 t^3 \) to ease the coordiantes to integer values. Makes the transition between cells more smooth.

Then, at the lattice point of each of the corners of the unit cube, a gradient vector is assigned. The vector is defined using precomputed random numbers that are looked up in a permutation table using the lattice indicies. This ensures that we will have the same gradient vectors everytime we sample within the same lattice. How this permutation table is computed i do not know but i do know that a Monte-carlo simulation was used “to compute 256 gradient vectors uniformly around the surface of a sphere.” (Presentation by Ken Perlin)

Given these gradients the current point is evaluated by using the current coordinates in an interpolation between all of the corner gradients. A gradient pointing away from the current position means a negative contribution while a gradient pointing towards the current position means a positive contribution.

A 2D example of perlin noise, with lattice borders and gradients illustrated is shown below:

Implementation

First i tried to implment the algorithim in matlab in order to quickly be able to generate visual results. When finished the implemenation was extremly slow so, next the algortihm was implemented in c with the purpose of interfacing nicley with our existing shader, which resulted in a much faster implementation.

Next, a simple c program which genrates a file of random values using perlin noise was written which I then could parse using matlab and display a picture of the noise in order to verify. Resulting 2D perlin noise from our implementation can be seen below:

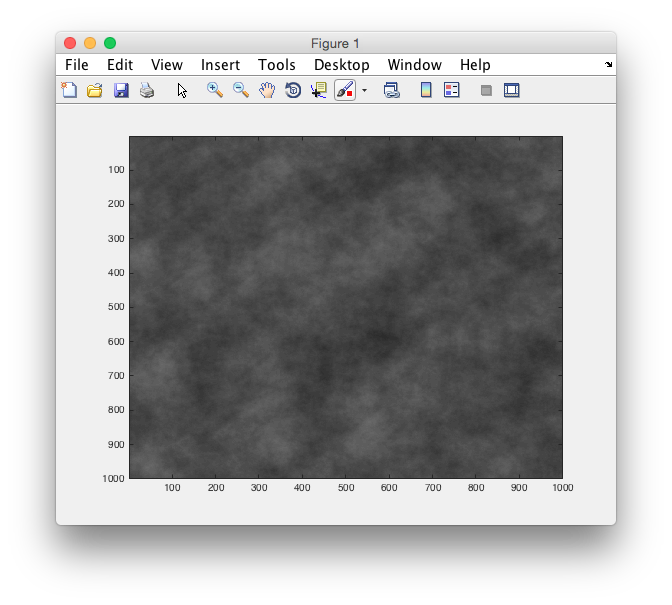
Kepping two of the input coordinates that are provided to the perlin noise function fixed results in 1 dimensional perlin noise, which is more of intereset for our puroses:

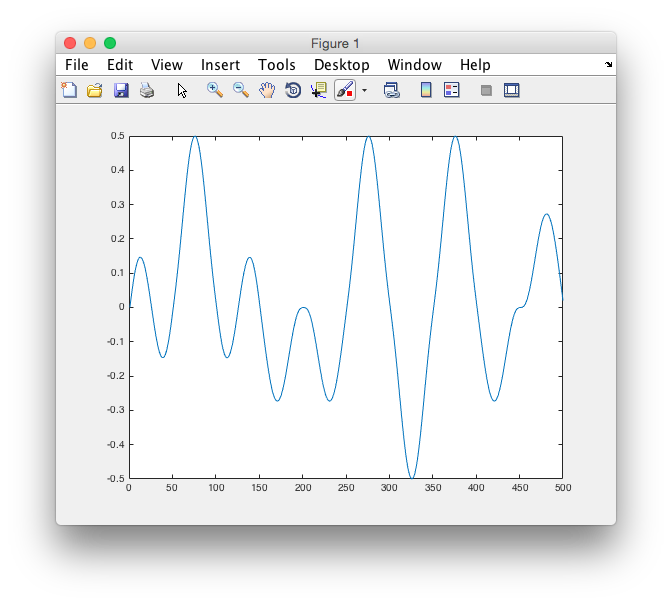
Hooking it up to the the shader

We now have access to smooth and natural looking noise!

Using the different thread coordinates we have access to the diffuse intesnity of a yarn can be varied along its length. First we do the usual swap of x and y if we are on a weft to ensure that y alwasy goes along the length of the yarn and x across it.

Then the x integer index of the current pattern is used as the x coordiante input for the noise function, while the y input is a continious floating point value. This way the variation only changes along the length of a yarn, but the variation is diffrent on parallel yarns.

To ensure that the difference between parallell yarns is large enough the x coordinate is scaled.

    static float yarnVariation(wcPatternData pattern_data, 
            const wcWeaveParameters *params)
    {
        float variation = 1.f;

        uint32_t tindex_x = pattern_data.total_index_x;
        uint32_t tindex_y = pattern_data.total_index_y;

        //Switch X and Y for warp, so that we have the yarn going along y
        if(!pattern_data.warp_above){
            float tmp = tindex_x;
            tindex_x = tindex_y;
            tindex_y = tmp;
        }

        //We want to vary the intesity along the yarn.
        //For a parrallel yarn we want a diffrent variation. 
        //Use a large xscale to make the values different.
        
        float xscale = 500.f;  //parameter
        float yscale = 0.2;  //paramater
        float amplitude = 1.f;  //paramater
        int octaves = 1; //paramter
        float persistance = 0.3; //paramter

        float x_noise = (tindex_x/(float)params->pattern_width) * xscale;
        float y_noise = (tindex_y + (pattern_data.y/2.f + 0.5))
            /(float)params->pattern_width * yscale;

        variation = octavePerlin(x_noise, y_noise, 0,
                octaves, persistance) * amplitude + 1.f;

        return wcClamp(variation, 0.f, 1.f);
    }

Results

Doing a quick check in the yarnVariation one can restrict variation to either wefts or warps which also gives nice results.

An example with varation restricited to wefts and a smaller yscale.

An example with varation restricited to wefts and a longer yscale.